5. Tutorials¶
In this section, we provide detailed tutorials for the main features of the Spex code.
5.1. GW calculations¶
The Spex code was started as a pure GW code. The GW approach remains the main computational method implemented in the code.
5.1.1. One-shot GW approach¶
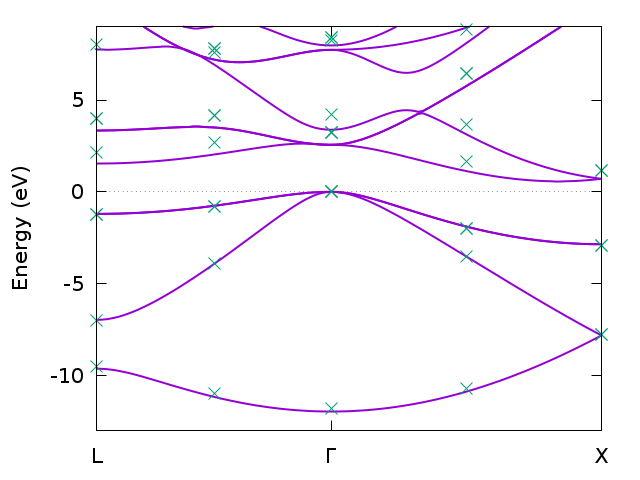
A simple input file for a one-shot GW calculation for bulk silicon was already presented in Section 2. The following, equivalent input file is even more minimalistic.
BZ 4 4 4
JOB GW 1:(1,2,5) 7:(1,3,5) 3:(1-3,5)
It only contains the two essential keywords that any Spex input file must contain: BZ and JOB, specifying, respectively,
the k mesh for the Brillouin-zone sampling and the requested type of calculation. Here, we calculate quasiparticle corrections
for the bands (1,2,5) at the first, (1,3,5) at the seventh, and (1,2,3,5) at the third k point. The band indices are defined
according to the ordering in the mean-field input data. In the example, we have left out some band indices because of energy
degeneracy. For example, bands 3 and 4 (of the first k point) are degenerate with band 2.
In the case of a spin-polarized system, Spex calculates the quasiparticle energies for both spins by default.
Alternatively, one can choose the spin index by using u (spin up) or d (spin down), e.g., JOB GW 1:u(1,2,5) 1:d(1,2,5)
is identical to JOB GW 1:(1,2,5).
The same definition of bands is used for the job types HF, PBE0, SX, COSX, GT, GWT, and KS.
For example, JOB COSX 1:(1,2,5) would run a COHSEX calculation. Many of the keywords described in this section
work identically for the other job types, others can only be used for GW calculations. If a keyword is inapplicable to the
defined job, it is simply ignored by Spex (e.g., SPECTRAL for a PBE0 calculation).
5.1.2. KPT¶
The k points follow an internal ordering: first the irreducible (parent) k points, then the remaining equivalent k points. A list of the irreducible k-vectors is written to the output file. In the present example, there are eight irreducible k points and 64 k points in total. All 64 k-point indices can be used in the job definition. We have chosen the ones from the irreducible set. They correspond to the \({\Gamma}\) (index 1), X (index 7), and L point (index 3). Clearly, for a different k-point set, e.g., \(8\times 8\times 8\), the k-point indices would change (except for the index 1, which always corresponds to the \({\Gamma}\) point). Therefore, there is the possibility of defining k-point labels by
KPT X=1/2*(0,1,1) L=1/2*(0,0,1)
or
KPT X=[1,0,0] L=1/2*[1,1,-1]
The labels can be ten characters long and may include upper- and lower-case characters, numbers, and also special characters except
blanks. Of course, the labels must not be integer numbers. Fractions can also be used inside the brackets, e.g., X=(0,1/2,1/2)
would be identical to the first k-point label. The two KPT definitions shown above are equivalent.
The first gives the k vectors in internal coordinates, i.e., in the basis of the reciprocal basis vector,
the second in cartesian coordinates in units of \({2\pi/a}\) with the lattice constant \(a\). In the case
of the fcc lattice of silicon, the lattice basis vectors are \({a_1=a(0,1,1)/2}\) , \(a_2=a(1,0,1)/2\) ,
and \(a_3=a(1,1,0)/2\) . The reciprocal basis vectors are thus \({b_1=2\pi/a(-1,1,1)}\) et cetera.
For the X point, e.g., one then gets \({(a_2+a_3)/2=2\pi/a(1,0,0)}\) . In order for the cartesian
coordinates (square brackets) to be interpreted correctly, Spex obviously needs to know the lattice constant
\(a\).
(In Fleur, the lattice constant is taken to be the global scaling factor for the lattice vectors.)
The so-defined k points must be elements of the k mesh defined by BZ. We will later discuss how
points outside the k mesh can be considered using the special label +. With the k labels, the above
job definition can be written as JOB GW 1:(1,2,5) X:(1,3,5) L:(1-3,5) as in the input file described
in Section 2. There are two more special k-point labels: IBZ and BZ (e.g., JOB GW IBZ:(1,2,5))
stand for all k points in the irreducible and the full k set, respectively. (The label BZ is included
for completeness but is not needed in practice.) The IBZ label is helpful when a Wannier interpolation
of GW quasiparticle energies or
a self-consistent GW calculation is to be performed, which require the self-energy
to be calculated for the whole irreducible Brillouin zone.
The quasiparticle energies are written to standard output in tabular form:
Bd vxc sigmax sigmac Z KS HF GW lin/dir
1 -12.15897 -19.20415 6.60649 0.65146 -6.19011 -13.23529 -6.36401 0.73681
1.05993 -0.10556 -6.36806 0.72704
2 -13.30408 -14.45814 0.69809 0.76876 5.77669 4.62263 5.42615 0.00070
0.00039 -0.00088 5.42695 0.00081
5 -11.49631 -7.27160 -3.86726 0.76385 8.34013 12.56485 8.61313 -0.00731
-0.00708 -0.00533 8.61239 -0.00749
The columns are
Bdband index,vxcexpectation value of the exchange-correlation potential \(v^\mathrm{xc}\), e.g., -12.15897 eV,sigmaxexpectation value of the exchange self-energy \(\Sigma^x\), e.g., -19.20415 eV,sigmacexpectation value of the correlation self-energy \(\Sigma^c\), e.g., (6.60649+1.05993i) eV (note that the self-energy is complex),Zrenormalization factor \(Z\), e.g., (0.65146-0.10556i) eV,KSmean-field energy eigenvalue (e.g., from the previous KS-DFT calculation), e.g., -6.19011 eV,HFHartree-Fock value (one-shot), e.g., -13.23529 eV,GWGW quasiparticle values, e.g., (-6.36401+0.73681i) eV (linearized solution) and (-6.36806+0.72704i) eV (direct solution).
The two GW values for the quasiparticle energy follow two common methods to approximately solve the quasiparticle equation
where \({v^\mathrm{ext}}\), \({v^\mathrm{H}}\), \({\Sigma^\mathrm{xc}}\), \({\psi_{\mathbf{k}n}}\), \({E_{\mathbf{k}n}}\) are the external and Hartree potential, the GW self-energy, and the quasiparticle wavefunction and energy, respectively. Taking the difference \({\Sigma^\mathrm{xc}-v^\mathrm{xc}}\) as a small perturbation, we can write the quasiparticle energy as a correction on the mean-field eigenvalue
with the single-particle wavefunction \({\phi_{\mathbf{k}n}}\) and the frequency-independent potential
\({v^{\mathrm{xc}}}\), which in the case of a KS solution would correspond to the
local exchange-correlation potential; the nonlocal Hartree-Fock exchange potential and
the hermitianized self-energy of QSGW (see below) are other examples.
\({Z_{\mathbf{k}n}=[1-\partial\Sigma^{\mathrm{xc}}/\partial\omega(\epsilon_{\mathbf{k}n})]^{-1}}\) is called the renormalization factor. The two expressions on the right-hand side correspond to the “direct” (iterative) and “linearized” (non-iterative) solutions given in the output. The direct solution takes into account the non-linearity of the quasiparticle equation and is thus considered the more accurate result. However, there is usually only little difference between the two values.
Up to this point, the job syntax for Hartree Fock (JOB HF), PBE0 (JOB PBE0),
screened exchange (JOB SX), COHSEX (JOB COSX), and GT (JOB GT and JOB GWT)
calculations is identical to the one of GW calculations, e.g., JOB HF FULL X:(1-10).
(The keyword FULL is explained in Section 5.1.19.)
Except the latter (GT), all of these methods are mean-field approaches,
so one only gets one single-particle energy (instead of a ‘’linearized’’ and a ‘’direct’’ solution) for each band.
5.1.3. SPECTRAL (SENERGY)¶
(*) It should be pointed out that the quasiparticle energies given in the output rely on the quasiparticle approximation. The more fundamental equation, as it were, is the Dyson equation
which links the interacting Green function \(G\) to the non-interacting KS one \({G_0}\) and which, in principle, requires the self-energy to be known on the complete \({\omega}\) axis. The spectral function measured in photoelectron spectroscopy is directly related to the Green function by
where the trace (tr) is over the eigenstates and \({\epsilon_\mathrm{F}}\) is the Fermi energy.
The spectral function can be evaluated using the keyword SPECTRAL
in the section SENERGY.
Optionally, one can define a frequency mesh by
the keyword SPECTRAL in the section SENERGY, in the examples below from -10 eV to 1 eV in steps of 0.01 eV.
(The Fermi energy is at 0 eV.)
If there is no explicit mesh, Spex chooses one automatically.
The spectral function is then written to the file “spectral”,
one block of data for each k point given in the job definition.
There is another optional parameter given at the end of the line (third example below),
which can be used to bound the imaginary part of the self-energy and, thus,
the quasiparticle peak widths from below by this value (unset if not given).
This can be helpful in the case of very sharp quasiparticle peaks that are otherwise hard to catch with the frequency mesh.
The SPECTRAL keyword can be used in conjunction with band-structure calculations, see Section 5.1.14 for details.
SPECTRAL |
Write spectral function \({\text{Im}G(\omega)}\) to the file “spectral”; frequency mesh automatically defined. |
SPECTRAL {-10eV:1eV,0.01eV} |
Write spectral function on the specified frequency mesh (relative to the Fermi energy). |
SPECTRAL {-10eV:1eV,0.01eV} 0.002eV |
Bound imaginary part from below by 0.002 eV, preventing peak widths to become too small to be plotted. |
5.1.4. GW basics¶
Alhough GW calculations can be readily performed with the default settings, the user should be familiar to some degree with the details of the computation and how he/she can influence each step of the program run. Also note that the default settings might work well for one physical system but be unsuitable for another. To lay the basis for the subsequent sections, we briefly recapitulate the basics of the GW method.
The GW self-energy
can be understood as a scattering potential that contains the exact exchange potential and correlation effects through the inclusion of \(W\), the dynamically screened interaction, which incorporates the screening of the many-electron system into an effective dynamical potential, obtained from the dielectric function \(\varepsilon\) through
This integral equation turns into a matrix equation
if the quantities \({W}\), \({\varepsilon}\), and \({v}\) are represented in the mixed product basis (Section 6.2), which thus has to be converged properly. The dielectric function, in turn, describes the change of the internal potential through screening processes and is related to the polarization matrix by \({\varepsilon(\mathbf{k},\omega)=1-P(\mathbf{k},\omega)v(\mathbf{k})}\) in matrix notation. The polarization function is one of the main quantities in the GW scheme. Its evaluation is described in Section 5.2.
The self-energy can be written as the sum of two terms, the first of which is the exact non-local exchange potential of Hartree-Fock theory, the remainder can be interpreted as a correlation self-energy and has the mathematical form of Eq. (3) with \({W(\omega)}\) replaced by \({W^\mathrm{c}(\omega)=W(\omega)-v}\). The frequency integration is carried out analytically for the exchange part (by summing over the residues). The correlation part is more complex to evaluate because of the frequency dependence of the interaction. (Fast electrons experience a different potential than slow electrons.)
There are several ways to represent the self-energy as a function of frequency. The default method is analytic continuation, in which the screened interaction and the self-energy are evaluated on a mesh of purely imaginary frequencies. The self-energy is then analytically continued to the complete complex frequency plane (\({\Sigma^\mathrm{xc}(i\omega)\rightarrow\Sigma^\mathrm{xc}(z)}\), \({\omega\in\cal{R}}\), \({z\in\cal{C}}\)). This has several advantages over the usage of the real frequency axis. First, \({W(\omega)}\) is a hermitian (or real-symmetric) matrix if \({\omega}\) is purely imaginary. Second, \(W\) and \({\Sigma^{\mathrm{xc}}}\) show a lot of structure along the real axis, whereas they are much smoother on the imaginary axis, thereby making it easier to sample and interpolate these functions. Third, after the analytic continuation the self-energy is known, in principle, as an analytic function on the complete complex plane. And fourth, the method requires only few parameters and is, therefore, easy to handle. The main disadvantage lies in the badly controlled extrapolation of the Padé approximants, which can sometimes produce “outlier values”, with a potential adverse effect on the accuracy and reliability of the method. Therefore, there is a more sophisticated but also more complex method called contour integration, in which the frequency convolution is performed explicitly, yielding the self-energy directly for selected frequencies on the real axis. This method requires the screened interaction \(W\) to be calculated in a small range on the real frequency axis, another contribution comes from an integration along the imaginary frequency axis. As a third alternative, there is a hybrid method that is nearly as accurate as the “explicit” contour integration method, but it is faster and avoids the calculation of \(W\) for real frequencies altogether.
5.1.5. MESH (SENERGY)¶
All methods to calculate the self-energy employ a mesh of purely imaginary frequencies, which extends from 0 to some maximal \(i\omega_\mathrm{max}\).
The number of mesh points \(N\) and the maximal frequency must be provided as parameters, for example MESH 10 10.0,
which is the default. The mesh is defined by \({i\omega_n=i\omega_\mathrm{max}f_n/f_N}\) with \({f_n=\{(N-1)/[0.9(n-1)]-1\}^{-1}}\), \({n=1,2,...}\).
It is dense for small \({\omega}\), where the quantities have a lot of structure, and coarse for large \({\omega}\).
Sometimes it is helpful to make the mesh even finer for small \({\omega}\). This is possible by specifying, for example, 10+3,
which would yield three, two, and one extra equidistant frequencies in the ranges [\({\omega_1,\omega_2}\)], [\({\omega_2,\omega_3}\)],
and [\({\omega_3,\omega_4}\)], respectively. If the second argument is defined negative (\({-\omega_\mathrm{max}}\)),
then \({f_n=\{N/(n-1)-1\}^{-1}}\). The latter definition is rarely used. One can also employ a user-defined mesh provided
in a file (one frequency per line, comments #... are allowed).
MESH 12 15.0 |
Use a mesh containing twelve frequencies for the range \([0,i15]\) htr. |
MESH 12+2 15.0 |
Add points at low frequencies, two (one) between \({\omega_1}\) and \({\omega_2}\) (\({\omega_2}\) and \({\omega_3}\)). |
MESH 12 -15.0 |
Use alternative mesh definition. |
MESH "mesh.dat" |
Read frequency mesh from file “mesh.dat”. |
5.1.6. CONTINUE (SENERGY)¶
The keyword CONTINUE (section SENERGY) chooses the analytic continuation method.
It can have optional parameters. If given without parameters (or if not specified at all),
Padé approximants are used. An integer number, such as CONTINUE 2,
lets Spex perform a fit to an n-pole function (here, n=2) with the Newton method.
The latter approach is somewhat obsolete by now and recommended only for test calculations.
The argument can have additional flags +, c, and *. Any combination is possible. They are explained in the examples.
CONTINUE |
Use Padé approximants (Default). |
CONTINUE 2 |
Fit to the two-pole function \({a_1/(\omega-b_1)+a_2/(\omega-b_2)}\). |
CONTINUE 2+ |
Include a constant in the fit function \({a_1/(\omega-b_1)+a_2/(\omega-b_2)+c}\). |
CONTINUE 2c |
Take constraints (continuity of value and gradient at \({\omega=0}\)) into account when fitting. |
CONTINUE 2* |
Allow parameters \({b_i}\) with positive imaginary parts (should be negative) to contribute. (Default with Padé method.) |
5.1.7. CONTOUR (SENERGY)¶
The second method is contour integration, in which the frequency integration is performed explicitly, however not along the real frequency axis but on a deformed integration contour that avoids the real frequency axis as best as possible. This integration contour starts from \({-\infty}\), describes an infinite quarter circle to \(-i\infty\), then runs along the imaginary frequency axis to \({i\infty}\), and finishes, again with an infinite quarter circle, to \(\infty\). The two quarter circles do not contribute to the integral (because the integrand behaves as \({\propto \omega^{-2}}\)). Furthermore, depending on the frequency argument \({\omega}\) of the self-energy, one has to add a few residues coming from the poles of the Green function in the interval \([0,\epsilon_\mathrm{F}-\omega]\) if \({\omega<\epsilon_\mathrm{F}}\) and \([\epsilon_\mathrm{F}-\omega,0]\) otherwise, which requires the correlation screened interaction \({W^\mathrm{c}(\omega)}\) to be evaluated on this interval of the real axis. As a consequence, the calculations are more demanding in terms of computational complexity and cost (time and memory). Also, contour integration requires additional input parameters and is therefore somewhat more difficult to use. However, the results are more accurate. In particular, they are not affected by the “ill-definedness” of the analytic continuation.
The corresponding keyword is called CONTOUR and belongs to the section SENERGY.
Obviously, CONTOUR and CONTINUE must not be given at the same time. The keyword CONTOUR expects two arguments.
The first defines the frequencies \({\omega}\), for which the self-energy \({\Sigma^\mathrm{xc}(\omega)}\)
is to be evaluated. At least, two frequencies are needed to approximate the self-energy as a linear function in \({\omega}\) and,
thus, to calculate the ‘’linearized’’ solution of the quasiparticle equation [Eq. (2)]). For this, a single value suffices
(example 0.01), with which the self-energy for a state \({\mathbf{k}n}\) is evaluated at two frequencies
(\({\epsilon_{\mathbf{k}n}-0.01}\) htr and \({\epsilon_{\mathbf{k}n}+0.01}\) htr).
The more accurate ‘’direct’’ solution is only available if we specify a range of frequencies for the self-energy instead of a single number,
making an interpolation of the self-energy beyond a linear function possible.
This is possible by an argument such as +-{-0.1:0.15,0.01}. Here, the range of values is relative to \(\epsilon_{\mathbf{k}n}>\epsilon_\mathrm{F}\).
The range is reversed (to -0.15:0.1 in the example) for occupied states (\(\epsilon_{\mathbf{k}n}<\epsilon_\mathrm{F}\))
to reflect the fact that occupied and unoccupied states tend to shift in opposite directions by the renormalization.
(Thus, it makes sense to choose a frequency range shifted to larger energies instead of a symmetrical one.)
One can also specify an absolute frequency mesh, example {-0.3:0.3,0.01}, where the energies are given relative to the Fermi energy.
Defining such an absolute frequency mesh is mandatory for calculations combining CONTOUR with FULL (Section 5.1.19).
It is sometimes a bit inconvenient to determine suitable values for the upper and lower bound of {...}.
Therefore, Spex allows the usage of wildcards for one of the boundaries or both (see examples).
The lower (upper) bound is then set at 0.07 htr below (above) the lowest (highest) mean-field band energy defined in the JOB GW line.
The “margin” of 0.07 htr is added to avoid that the renormalization pushes the quasiparticle energy beyond the frequency grid.
It is also possible to define the margin explicity. For example, {*-0.07:*+0.07,0.01} would be
identical to {*:*,0.01}.
The second argument to CONTOUR gives the increment of the (equidistant) real-frequency mesh for \({W(\omega')}\).
The lower and upper boundaries of this mesh are determined automatically from the first argument. As a third method,
Spex also allows the second argument to be omitted altogether. Then, it uses a hybrid method where the screened interaction is
analytically continued from the imaginary axis (where it has to be known for the evaluation of the integral along this axis, see above) to the real axis,
thereby obviating the need of calculating and storing W on a real-frequency mesh.
The disadvantage is that the badly controlled Padé extrapolation introduces an element of randomness
(also see keyword SMOOTH below). Our experience so far is that the hybrid method is in-between the two other methods
in terms of both computational cost and numerical accuracy.
CONTOUR 0.01 0.005 |
Use contour integration to obtain the two values \({\Sigma^\mathrm{xc}(\epsilon\pm 0.01\,\mathrm{htr})}\) with the KS energy \(\epsilon\), giving \({\Sigma^\mathrm{xc}}\) as a linear function. |
CONTOUR +-{-0.1:0.15,0.01} 0.005 |
Calculate \({\Sigma^\mathrm{xc}(\omega)}\) on a frequency mesh relative to the KS energy \({\epsilon}\). |
CONTOUR {*:*,0.01} 0.005 |
Use an absolute frequency mesh (relative to the Fermi energy) instead. Wildcards are used for the upper and lower bounds. |
CONTOUR {*:*,0.01} |
Use hybrid method. |
CONTOUR {*-0.1:*+0.1,0.01} |
Use hybrid method with a different margin of 0.1 htr (see text). |
Note
Until version 05.00pre31, the syntax was {...} for +-{...} and [{...}] for {...}.
5.1.8. FREQINT (SENERGY)¶
(*) Independently of whether \({\Sigma^\mathrm{xc}(i\omega_n)}\) (CONTINUE) or \({\Sigma^\mathrm{xc}(\omega_n)}\) (CONTOUR) is evaluated,
an important step in the calculation of the self-energy is to perform the frequency convolution
\({\int_{-\infty}^\infty G(z+i\omega')W(i\omega')d\omega'}\) with \({z=i\omega_n}\) or \({z=\omega_n}\).
For this frequency integration, we interpolate W and then perform the convolution with the Green function analytically.
The keyword FREQINT determines how the interpolation should be done. It can take the two arguments SPLINE (default) and PADE
for spline [after the transformation \({\omega'\rightarrow \omega'/(1+\omega')}\)] and Padé interpolation, respectively.
In the case of GT calculations, there is a similar frequency integration with the T matrix replacing W.
An experimental option is NONLIN, which invokes a new tetrahedron k integration method that uses weight functions instead of
weight factors. This enables smooth integrations over strongly varying (highly nonlinear) functions, which is particularly useful
for the magnetic T matrix with its very sharp spin-wave peaks. Therefore, the default for GT calculations is NONLIN.
FREQINT NONLIN, in particular, affects the calculation of the residues
part in a CONTOUR calculation but also the integration along the imaginary frequency axis (both for CONTINUE and CONTOUR),
where it uses Padé interpolation. We note that FREQINT NONLIN and, to a lesser extent, also FREQINT PADE tend to break energy
degeneracies slightly.
FREQINT SPLINE |
Use spline interpolation for W (or T) in the frequency convolution \({G\cdot W}\) (\({G\cdot T}\)) (default for GW). |
FREQINT PADE |
Use Padé interpolation. |
FREQINT NONLIN |
Use new tetrahedron k integration method (default for GT). |
5.1.9. SMOOTH (SENERGY)¶
(*) We have already mentioned that the Padé approximation can lead to spurious features in the extrapolated or interpolated quantity,
i.e., the self-energy or the screened interaction (also see FREQINT), if one of the Padé poles happen to lie close to the real
(or imaginary) frequency axis. To avoid such unphysical results, we can make use of an averaging procedure where,
for each set of values, \({\{\Sigma^\mathrm{xc}(i\omega_n)\}}\) or \({\{W(i\omega_n)\}}\),
we evaluate a large number of Padé approximants with randomly shifted frequency points according to
\({\omega_n\rightarrow\omega_n(1+10^{-7}r_n)}\) with random numbers \({r_n\in[-0.5,0.5]}\) and average over them.
This simple but effective way to smoothen the functions is activated with the keyword SMOOTH in section SENERGY.
It can have up to two arguments, giving the number of Padé approximants over which to average, the first for the self-energy,
the second for the screened interaction or the T matrix in the case of GT calculations (FREQINT PADE).
Smoothening is usually unnecessary for GW calculations but is helpful in the case of the GT approach.
By default, no smoothening is applied. Note that this feature leads to a small degree of randomness in the results.
SMOOTH 500 |
Average over 500 Padé approximants to smoothen the self-energy. |
SMOOTH 500 250 |
In addition, average over 250 approximants to smoothen W (or the T matrix). (Requires FREQINT PADE.) |
5.1.10. ZERO (SENERGY)¶
(*) Both the exchange (HF) and the correlation self-energy contain terms of the form
\(\langle...\rangle\langle...\rangle V(\mathbf{k})\)
with \({V=v}\) and \({V=W}\), respectively. The quantities \({\langle...\rangle}\) are the “projections” discussed in Section 6.2.
One of the involved projections acquires the form
\(\langle e^{i\mathbf{k}r} \phi_{\mathbf{q}n} | \phi_{\mathbf{k+q}n'} \rangle\), which
behaves as \({\propto k}\) in the long-wavelength limit \({k\rightarrow 0}\) and
\(n\neq n'\). The prefactor is obtained from \(k\cdot p\)
perturbation theory. Multiplying two of these projections with \(V\propto k^{-2}\) (or one with \(V\propto k^{-1}\),
which is valid for the “wings” of W) gives rise to zero-order terms.
These zero-order terms (which only appear at the \({\Gamma}\) point) can improve the k-point convergence.
However, in the case of systems with small band gaps, the zero-order terms can become unnaturally large
(because the integrand is strongly varying in the neighborhood of k=0 in such systems),
impeding a favourable convergence with respect to the k-point sampling.
The keyword ZERO (section SENERGY) includes the zero-order terms. They are neglected by default.
Note
Keyword ZERO replaces NOZERO of older versions (until 05.00pre31), which switched off zero-order corrections.
So, starting from version 05.00pre32, the default has changed to excluding zero-order corrections.
5.1.11. ALIGNVXC (SENERGY)¶
(*) Equation (1) depends explicitly on the mean-field starting point through the eigensolutions \({\{\phi_{\mathbf{k}n}\}}\).
This dependence is more obvious from Eq. (2), which contains the exchange-correlation potential explicitly.
Thus, a constant shift \({v^\mathrm{xc}\rightarrow v^\mathrm{xc}+\Delta}\) will not only shift the quasiparticle
energies as a whole (as it would the KS energies) but also individually so that energy differences (e.g., the quasiparticle band gap)
can depend on this constant shift. (Again, this is different from the KS gap, which would not be affected.)
The underlying reason is that quasiparticle energies represent total-energy differences (between the \(N\) and the \(N{\pm}1\) particle system)
and are thus defined as absolute energies, which depend individually on the “energy zero” set by \({v^\mathrm{xc}}\).
One can utilize this dependence to simulate the self-consistency condition that the input and output ionization potentials
(valence-band maximum) be identical; in other words, the ionization potential should not change by the quasiparticle renormalization.
The keyword ALIGNVXC in section SENERGY enforces this condition. To this end, the valence-band maximum should be included in the job definition.
(Spex uses the highest occupied one among the states defined after JOB for the correction.)
One can also specify the shift explicitly as a real-valued argument after ALIGNVXC. This is useful if a different criterion is to be used,
for example, requiring the Fermi energy (metallic case) or core state energies (core spectroscopy) to remain unchanged.
In this case, the shift has to be determined manually by repeatedly trying different shift values until the constancy of the desired quantity
is achieved (because the shift affects the results, so there is a feedback effect). In this trial-and-error approach, it is very helpful
to use RESTART 2 (Section 5.1.13), in which case the self-energy is read from harddisc and the calculation takes very little time.
ALIGNVXC |
Align exchange-correlation potential in such a way that the ionization potential remains unchanged by the quasiparticle correction. |
ALIGNVXC 0.2eV |
Apply a constant positive shift of 0.2 eV to the exchange-correlation potential. |
5.1.12. VXC (SENERGY)¶
(*) The matrix elements of the exchange-correlation potential are needed in the solution of Eq. (2).
By default, these matrix elements are calculated by Spex using the potentials from the input data.
Alternatively, they can be taken from data provided by the DFT code (e.g., in the file “vxcfull” written by Fleur).
For that, the keyword VXC in section SENERGY can take the arguments CALC (default) and READ.
(In some cases, VXC READ is not available, e.g., for PBE0 calculations.)
VXC READ |
Read \({v^\mathrm{xc}}\) expectation values from harddisc. |
VXC CALC |
Calculate \({v^\mathrm{xc}}\) expectation values using the xc potential defined in stars and lattice harmonics. |
5.1.13. RESTART¶
Spex can reuse data from a previous GW run that has finished successfully, crashed, or has been stopped by the user. (See Section 4.1.7 for more details.)
A GW calculation consists mainly of a loop over the irreducible k points. For each k point, Spex (a) calculates the matrix \(W(\mathbf{k})\) and (b) updates the self-energy matrix (or expectation values) \({\Sigma^\mathrm{xc}}\) with the contribution of the current k point (and its symmetry-equivalent k points). After completion of step (b), the current self-energy is always written to the (binary) files “spex.sigx” and “spex.sigc”. If the RESTART option is specified (independently of its argument), Spex also writes the matrix \(W(\mathbf{k})\) (in addition to some other data) to the (HDF5) file “spex.cor” unless it is already present in that file. If it is present, the corresponding data is read instead of being calculated. In this way, the keyword RESTART enables reusage of the calculated \(W(\mathbf{k})\) from a previous run. The matrix \(W(\mathbf{k})\) does not depend on the k points and band indices defined after JOB. So, these parameters can be changed before a run with RESTART, in which the W data is then reused.
For example, band structures can be calculated efficiently in this way (Section 5.1.14).
Especially for long calculations, it is recommended to use the RESTART option.
Spex can also restart a calculation using self-energy data contained in “spex.sigx” and “spex.sigc”.
To this end, the argument 2 is added: RESTART 2. Spex then starts with the k point, at which the calculation was interrupted before.
In contrast to “spex.cor”, the files “spex.sigx” and “spex.sigc” do depend on the job definition,
which must therefore not be changed before a run with RESTART 2.
However, there are few parameters (see below) that may be changed before a rerun with RESTART 2.
These concern details about how the quasiparticle equation is solved after completion of the self-energy calculation. The following logical table gives an overview.
spex.cor |
spex.sigx/c |
|
|---|---|---|
| – | – | write |
RESTART |
read-write | write |
RESTART 2 |
read-write | read-write |
The different rules for “spex.cor” and “spex.sigx/c” are motivated by the facts that (a) the file “spex.cor” is much bigger than “spex.sigx/c” (so, writing of “spex.cor” to harddisc should not be the default), (b) the files “spex.sigx/c” include the updated self-energy (requiring more computation than for W, thus representing “more valuable” data).
There are other (binary) files that are written during a program run and that may be reused later. The ones relevant for GW (same rules as for “spex.cor”) are
spex.mb: contains MT part of product basis,spex.ccou: contains “contracted” screened interaction (i.e., summed over k); this contraction is needed for the self-energy core contribution (CORES), forCOSX, and forIBC,spex.core: contains core contribution to W (keywordCORES, Section 5.1.18).
The RESTART option can be exploited to customize the calculations. For example, it is possible to perform a self-consistent QSGW calculation
while keeping W fixed to the LDA level throughout the iterations. (The screened interaction is then always read from “spex.cor” and the MT product basis from “spex.mb”.) As another example, when CORES is used, the MT product basis additionally contains products of core states with LAPW basis functions. To avoid that, one can run a calculation without CORES first (which can be stopped just after the product basis is written to “spex.mb”), followed by a calculation with RESTART. The product basis is then read from “spex.mb” (excluding the core-basis products) instead of being constructed anew.
As already mentioned above, changing input parameters in “spex.inp” and running a calculation with RESTART might lead to a conflict
between the changed parameters and the data read from the restart files.
Spex tries to detect such conflicts. In case of conflict, Spex either stops the calculation (“spex.cor”) or recalculates the data and overwrites the files (“spex.sigx/c”). It is, however, not guaranteed that Spex can detect all possible conflicts. So, care has to be taken if parameters are changed in calculations with RESTART.
The following is a (incomplete) list of parameters that may be changed for a calculation with RESTART 2, in which the files “spex.sigx/c” are read:
ALIGNVXC, VXC, SPECTRAL, SMOOTH, CONTINUE, WRITE, all of section WANNIER (e.g., for Wannier interpolation).
In the case of RESTART 1 (or just RESTART) (i.e, when “spex.cor” is to be read), one may change most parameters except: MESH, 2nd argument of CONTOUR, JOB types (most cases). Many changes of parameters will be overridden with values from the restart files (e.g., parameters in the section MBASIS by data from the file “spex.mb”). Other changed parameters might affect only the self-energy but not the
screened interaction W, for example, NBAND. (The latter allows the band convergence of W and \({\Sigma^\mathrm{xc}}\) to be checked separately.) Again, this can be used efficiently to customize a calculation.
RESTART |
Spex tries to read the screened interaction W (and other data) from the file “spex.cor”. If the required data does not exist, the calculation proceeds normally and appends W to the file (reusable in a later restart). |
RESTART 1 |
Same as RESTART. |
RESTART 2 |
Implies RESTART. Spex reads the self-energy from the files “spex.sigx” and “spex.sigc” if they exist. If not, the calculation proceeds normally. |
5.1.14. GW band structures¶
In this section, three ways of calculating GW band structures are discussed.
- Using the
KPTPATHlabel (single Spex run, Section 5.1.15), - With the special
+label inKPTfor additional q points (multiple Spex runs, Section 5.1.16), - Wannier interpolation (single – but long – Spex run, Section 5.1.17).
The calculation of a GW band structure is not as straightforward as in the case of KS-DFT, where the local nature of the effective potential (e.g., LDA or GGA) allows the KS Hamiltonian to be diagonalized independently for each q point along a q-point path.
The GW self-energy, on the other hand, is non-local. As a consequence,
its evaluation involves a convolution in reciprocal space
\({\Sigma^\mathrm{xc}(\mathbf{q})=i\sum_\mathbf{q}G(\mathbf{q+k})W(-\mathbf{k})}\) (in simplified notation),
requiring summations over the full Brillouin zone for any arbitrarily chosen q point. So, in addition to \(\mathbf{q}\),
one would need to include all shifted points \(\mathbf{q}+\mathbf{k}\), as well, where \(\mathbf{k}\) stands for the k points defined in BZ.
If we restrict ourselves to the set of k points defined in BZ, the band structure along a certain high-symmetry line (e.g., \({\Gamma-X}\))
can consist only of the few k points that happen to lie on this line. Sometimes this is already sufficient. For example, if the GW renormalization
affects the band dispersion only little, then a few points along the high-symmetry line are enough to shift/modify the KS bands accordingly and produce,
in this way, a quasiparticle band structure. Such a calculation can be performed in a single Spex run.
5.1.15. KPTPATH¶
As an example, we want to plot a band structure for the path from L over \(\Gamma\) to X for our Si example.
In principle, we would have to identify all k-point indices along this path and set the job definition accordingly,
but Spex can do this for you. The k-point path can be defined with a line KPTPATH (L,1,X).
(A user-defined set of k points can also be provided through a file, see examples.)
In the job definition,
one can then use the special label PATH to address the corresponding list of k points, e.g., JOB GW PATH:(1-10).
Spex will automatically choose the k points that lie on the path defined by KPTPATH and calculate the GW quasiparticle energies.
As usual, the results are written to the output file. The data can be extracted from the output file with the spex.extr utility:
spex.extr g -b spex.out > bandstr (assuming that the output has been piped into the file “spex.out”).
The file “bandstr” then contains a plottable list of xy values (momentum/energy) for each quasiparticle band.
However, in most cases the band structure will not be smooth enough because of the small number of k points.
One solution is, as already mentioned, to modify a KS band structure. Another possibility is to interpolate the energies with splines;
the spex.extr utility has this capability. Finally, one could simply use much denser k-point sets, but this would entail very expensive calculations.
The keyword KPTPATH can also be used for the other two methods to calculate a band structure (see Section 5.1.16 and Section 5.1.17).
In these methods, one is not restricted to the k points of the k set and can define k-point paths with arbitrary step sizes. To this end, an integer
argument can be specified at the end of the k-path definition. For example, KPTPATH (L,1,X) 50 would give a k path with a step size of (roughly)
\(K/50\), where \(K\) is the “average reciprocal lattice constant”, defined as \(K=2\pi/\sqrt[3]{\Omega}\) with \(\Omega\) the volume
of the unit cell. The actual step size between the defined k points (L, \(\Gamma\), and X in the example) is adjusted in such a way that these k points
lie on the path (hence the use of the word “roughly” above).
Larger integer arguments give denser k meshes. The default is 20 for the method explained in Section 5.1.16 and 100 for the one in Section 5.1.17.
KPTPATH (L,1,X) |
Define k-point path from L over the \(\Gamma\) point (k index is always 1) to X. The labels L and X must be defined with KPT. |
JOB GW PATH:(1-10) |
Run GW calculation for the first ten bands at all k points defined by KPTPATH. |
KPTPATH (1,N) 100 |
Define k-point path from \(\Gamma\) to N and use step size of \(2\pi/(100\sqrt[3]{\Omega})\). |
KPTPATH "my_kpath" 100 |
Read k-point path from file “my_kpath”. |
5.1.16. KPT +=…¶
This section explains an extension to the keyword KPT (Section 5.1.2), which will later enable the calculation of smooth band structures.
The extension enables adding arbitrary q points, one at a time, allowing one to investigate the quasiparticle spectrum at momenta that
are not element of the original k-point set (defined by BZ).
For example, in Si the conduction-band minimum is not at a high-symmetry k point but at around 3/4 along the line \({\Gamma - \mathrm{X}}\).
This particular q point can be defined using the special k label “+” by +=[0,0,0.75] (alternatively, +=3/8*(1,1,0) in internal coordinates)
after the keyword KPT. As explained above, each additional point \(\mathbf{q}\) must in principle be accompanied with all shifted points \(\mathbf{q}+\mathbf{k}\).
So, before running Spex, we must let the DFT code generate the wavefunctions and energies at the shifted k-point set \(\{\mathbf{q}+\mathbf{k}\}\).
This is done in the usual way by creating the k-point file (Section 4.1.2) and running the DFT code.
(In the case of Fleur, the shifted k points are appended to the list in the file “kpts”.)
The additional q point can be addressed in the job definition with the special “+” label, e.g., JOB GW 1:(1-5) +:(1-5),
which will yield the bands 1-5 for the \(\Gamma\) point and the additional q point.
The energy difference between the fourth state at \(\Gamma\) and the fifth state at \(\mathbf{q}\) yields the fundamental GW gap.
KPT +=1/7*[1,0,0] |
Define special k point at 1/7 along the line \({\Gamma - \mathrm{X}}\) (here, the X point in x direction) of an fcc structure. |
KPT +=1/14*(0,1,1) |
The same in internal coordinates. |
JOB GW +:(1-10) |
Run GW calculation for the states 1-10 at the added q point. |
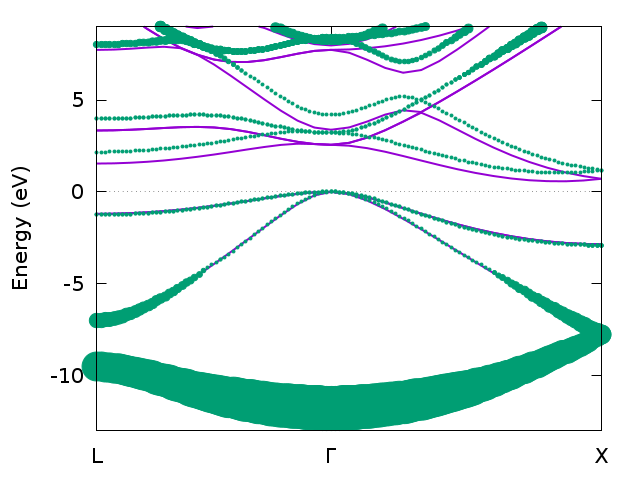
Band structure for bulk silicon from DFT (magenta) and GW (green) calculated with multiple runs of Spex using the “spex.band” shell script.
The possibility of adding arbitrary q points enables the calculation of smooth band structures.
To this end, a GW run (together with the generation of the eigenstates with the DFT code)
has to be performed for each q point in a list of q points that make up a path in the Brillouin zone,
e.g., from \({\Gamma}\) to \(X\). This list is defined with the keyword KPTPATH as explained above.
Fortunately, the screened interaction has to be calculated only once and can be reused for the other points.
For this, the keyword RESTART should be given in the input file. Of course, we also need a job definition,
such as JOB GW +:(1-10). Here, only the additional q point should be specified. It would be difficult to
extract the data for the band structure plot otherwise.) Now, running Spex with KPTPATH defined in the input
file and WRTKPT (or with the command line option -w) creates two files, containing the usual list of
k points (Fleur: “kpts”) and the list of q points (Fleur: “qpts”). For each of the q points, we would have to run,
in this order, Spex, Fleur, and Spex again. To simplify this task, there is a shell script called “spex.band”.
This shell script performs all the necessary steps automatically. It uses the same environment variables as “spex.selfc” (Section 5.1.19)
and produces, for each q point, one output file named “spex_NNN.out”, where NNN is a three-digit counting index, or more digits if the index exceeds 999.
From these files the band-structure data is extracted with spex.extr g -b spex_???.out > bandstr.
The data is written to the file bandstr. The band structure can then be plotted with “xmgrace” or “gnuplot”.
If you extract the band-structure data, instead, with spex.extr g -b -c spex_???.out > bandstr,
you get an additional column, which contains the imaginary parts of the quasiparticle energies.
These imaginary parts are proportional to the line width and inversely proportional to the excitation lifetime.
The line widths can be plotted together with the band structure in “gnuplot” with plot "bandstr" using 1:2:(10*abs(3)) with points ps var.
You will see that the bands get wider the further they are away from the Fermi energy.
If “spex.inp” contains a SPECTRAL definition (Section 5.1.3), the script “spex.band” also renames the file “spectral”,
written in each Spex run, to “spectralNNN” with the same counting index NNN as above. The spectral data can
be compiled with the “spex.extr” utility (e.g., spex.extr s -b spectral??? > spec)
into a single data file containing a list of xyz value triples: the Bloch momenta as the first column, the frequency as
the second, and the value of the spectral function as the third. With “gnuplot”, for example,
a momentum-frequency plot of the spectral function with color coding is then prepared with the command
plot "spec" using 1:2:3 palette with lines. (The respective color range is set with set cbrange [...],
see the Gnuplot manual.)
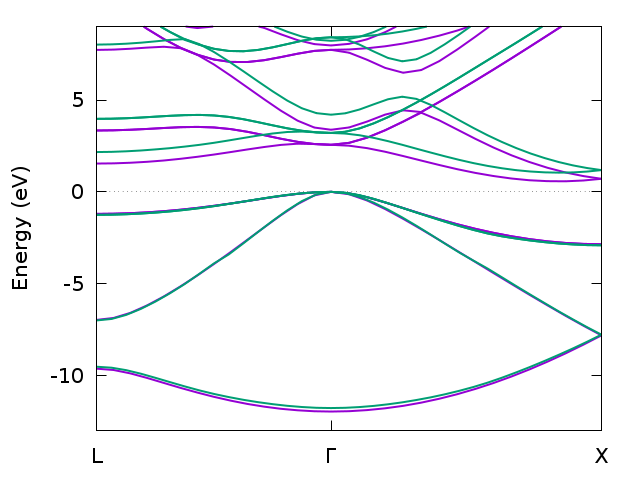
5.1.17. INTERPOL¶
As a third alternative, we can use Wannier interpolation to interpolate between the few k points of the original k mesh.
The construction of Wannier orbitals is explained in Section 6.3. Here, we use a minimalistic definition for demonstration purposes.
We have to modify and add some lines to spex.inp:
JOB GW IBZ:(1-4)
SECTION WANNIER
ORBITALS 1 4 (sp3)
MAXIMIZE
INTERPOL
END
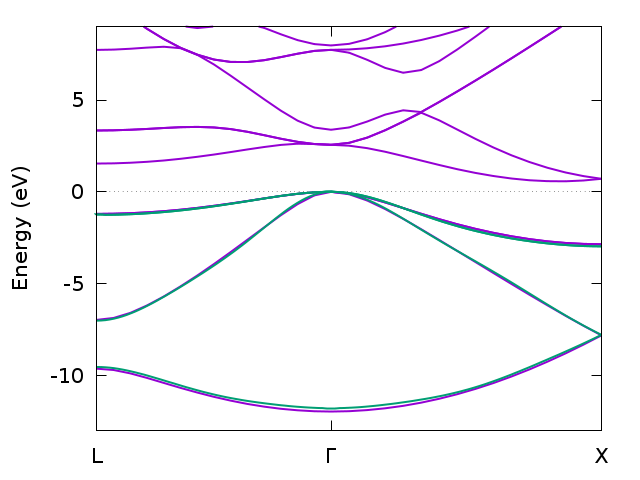
Band structure for bulk silicon from DFT (magenta) and GW (green) calculated with Wannier interpolation (only filled bands).
Please also remove the entry +=[0,0,0.75] from the KPT line. The first line lets SPEX calculate quasiparticle energies
in the whole irreducible Brillouin zone (IBZ). (The Wannier interpolation can be understood as a back-and-forth Fourier
transformation with a real-space truncation of matrix elements in-between.
The Fourier transformation from momentum to real space involves the band energies in the whole BZ.)
The section WANNIER defines a set of maximally localized Wannier functions (MLWFs) of bonding sp3 hybrid orbitals.
These four hybrid orbitals are generated from the four lowest valence bands (first two arguments after ORBITALS).
Running Spex will construct the MLWFs and use them to interpolate the band structure.
The band structure data is written to the files “bands0” for the KS energies and “bands1” for the GW quasiparticle energies
and can be plotted with “xmgrace” or “gnuplot”. The file “bands1” has one data column more than “bands0”.
This additional column contains the interpolated imaginary parts of the quasiparticle energies.
You can plot the band structure with the line thickness scaled by the imaginary part in the same way as described before.
The band structure is calculated along the k-point path defined by KPTPATH (Section 5.1.15).
Alternatively, one can specify a file after INTERPOL, e.g., INTERPOL "qpts".
The k-point path is then taken from that file. (The file structure is the same as that of the file “qpts” written by
spex -w when KPTPATH is defined. 1st line: number of k points, common denominator; 2nd, 3rd, … lines:
k points defined as three-tuples.)
Wannier interpolation can also be used in conjunction with the keyword SPECTRAL (Section 5.1.3).
The interpolated spectral function is written to the file “spectralw” or, if the system is spin-dependent,
to the files “spectralw1” and “spectralw2” for the spin up and spin down channels, respectively. These files
can be plotted in the same way as described in Section 5.1.16.
The plot of “fat bands” (orbital projections) is possible in combination with the keyword PROJECT (Section 4.2.3).
By default, the projection onto Wannier orbitals (“Wannier projections”) are given for each state in the output file (e.g., “bands0”).
Further details about Wannier functions are found in Section 6.3 and some practical advice on Wannier interpolation in Section 6.3.7.
5.1.18. CORES¶
By default, the n summation in the Green function
for the self-energy [Eq. (3)] includes only the valence and conduction states represented in the LAPW basis but excludes the core states.
In theory, of course, the core states should be included. Their contribution is, however, numerically small. Spex allows selective core states
to be included in the evaluation of the self-energy with the keyword CORES. This keyword also affects the calculation of the polarization function, see
Section 5.2.4. As arguments, Spex expects a comma separated list of core states between round brackets, e.g., (2s,2p,3d), for each atom type.
Empty definitions () are allowed. If CORESOC is specified, one can also address the SOC-splitted states individually, e.g., (2p1/2).
CORES () (1s) |
Include the 1s state of the second atom type. |
CORES (2s,2p1/2) |
Include the 2s and the 2p1/2 states but exclude the 2p3/2 states. |
5.1.19. Beyond perturbative GW and QSGW¶
One can also go beyond the perturbative solution of Eq. (1) and solve this equation by iterative diagonalization
in the basis of the single-particle states.
This requires the full self-energy matrix including off-diagonal elements to be calculated.
The respective line in the input file would read JOB GW FULL 1:(1-10) X:(1-10) L:(1-10)
giving the self-energy as \(10\times 10\) matrices at the \(\Gamma\), X, and L points.
(In principle, it is also possible to have a band definition like (1-5,9,10), which would yield a \(7\times 7\) matrix.
Degenerate states, not included in the definition, are automatically included.)
In FULL calculations, the Spex code uses irreducible representations (irreps) to speed up the calculation.
As a result, the bands are grouped in terms of these irreps (called “blocks”) in the output.
For example, in the example below (for the X point) the block is composed of the bands 3, 4, 9, and 10.
If a block contains only a single band or a single subgroup of degenerate states,
the full solution is omitted because it would be identical to the perturbative (diagonal) solution.
The full solutions are tabulated in the output:
Bd KS olap HF olap GW
3 2.92306 0.99971 0.12683 0.99985 2.50496 -0.06006
4 2.92306 0.99971 0.12683 0.99985 2.50496 -0.06006
9 16.77136 0.99732 23.25660 0.99962 16.97051 -0.30294
10 16.77136 0.99732 23.25660 0.99962 16.97051 -0.30294
The values with the label HF are the Hartree-Fock values (from diagonalization).
They are not necessarily ordered according to energy but related to the KS states (with band indices labeled “Bd”)
with a condition of maximal overlap (and at the same time making sure that a one-to-one correspondence can be established).
The corresponding overlap is given on the left of the HF column.
The full GW energies (column labeled GW; the last column lists the imaginary parts) are related to the KS states as well.
This is due to the fact that the quasiparticle equation is non-linear in energy and must, therefore, be solved iteratively
for each quasiparticle state. The iterations are started with the corresponding KS energy \({\epsilon_{\mathbf{k}n}}\),
giving \({H^\mathrm{KS}+\Sigma^\mathrm{xc}(\epsilon_{\mathbf{k}n})-v^\mathrm{xc}}\)
as the (complex) quasiparticle Hamiltonian. The diagonalization then yields a spectrum of states,
of which the one with the largest overlap is picked for the next iteration. In the first few iterations,
the off-diagonal elements are switched on adiabatically to alleviate a smooth convergence.
The overlap of the final quasiparticle wavefunction with the original KS state is given, too.
Although, this approach usually yields well-defined quasiparticle solutions,
it cannot be ruled out that the iterative procedure, when started at two different energies,
might result in the same quasiparticle energy.
This can happen especially for states far away from the Fermi energy, which do not have a well-defined quasiparticle character anymore.
If the job definition contains FULL and IBZ, the full GW self-energy matrix is evaluated for the whole IBZ,
which enables self-consistent calculations in the framework of the quasiparticle self-consistent GW (QSGW) approach.
In this approach, one creates a mean-field system from the GW self-energy whose single-particle energies are as close
as possible to the quasiparticle energies. This mean-field system is subsequently solved to self-consistency in a DFT code.
The resulting solution can then serve as a starting point for a new one-shot GW calculation,
which constitutes the second iteration and so on until the quasiparticle energies are converged.
The construction of the mean-field system is, to some extent, arbitrary. We use the following definition,
which is slightly modified from the original work [Phys. Rev. Lett. 93, 126406]:
for diagonal elements and
for off-diagonal elements. The hermitianized QSGW operator is then obtained from \({\Sigma^\mathrm{xc,H}=(A+A^\dagger)/2}\). The difference to the original definition is the inclusion of the renormalization factor to better reproduce the GW quasiparticle energies. The hermitianized matrix, or rather the difference \({\Sigma^{\mathrm{xc,H}}-v^\mathrm{xc}}\), is written to the file “spex.qsgw”, which is later read by the DFT code. The exact procedure of a QSGW calculation depends on the DFT code used.
As an example, we explain the necessary steps for a calculation with Fleur v0.26b (2019.03):
rm fleur.qsgw- remove the file “fleur.qsgw” containing the hermitianized matrix used internally by Fleur from previous QSGW iterations.rm broyd*- remove Broyden information about previous iterations because this information is inconsistent with the new Hamiltonian (the SCF calculation does not converge otherwise).- Set
gw=3in the Fleur input file. - Run Fleur.
- Fleur translates the file “spex.qsgw” (in basis of eigenstates) to a file “fleur.qsgw” (in LAPW basis). Then, a SCF run is performed where, instead of the KS Hamiltonian \({H^\mathrm{KS}}\), the Hamiltonian \({H^\mathrm{KS}+(\Sigma^{\mathrm{xc,H}}-v^\mathrm{xc})}\) is employed. After the run finishes, the
gw=2step has to be performed.
- Set
gw=2in the Fleur input file. - Run Fleur.
Apart from the usual output data for a GW calculation, Fleur writes, in addition, the file “qsgw”, which contains the matrix elements of
\({\Sigma^{\mathrm{xc,H}}-v^\mathrm{xc}}\) in the basis of the new eigenstates. The file “qsgw” is later read by Spex to subtract the double counting.
Of course, doing these steps manually is tedious and error-prone. Therefore, we provide the shell script spex.selfc,
which performs the steps needed for a self-consistent calculation automatically. For example, spex.selfc 5 will run five iterations.
The shell script assumes that Spex and Fleur are run with spex and fleur.x, respectively. Environment variables can be used to change this:
SPEX_EXEC- Spex executable,DFT_EXEC- Fleur executable,SPEX_THRU- Command to prepend Spex executable (e.g., queue command or MPI launcher such asmpiexec -np 20),DFT_THRU- Command to prepend Fleur executable.THRU- Default command to prepend Spex and Fleur executables.
The job types HF, PBE0, SX, and COSX also allow FULL in the definition, i.e., a full matrix is evaluated, enabling a self-consistent calculation in the same way as QSGW (see above). The file names used are the same: “spex.qsgw”, “fleur.qsgw”, “qsgw”, even though it might actually be a HF calculation. The job GT (also GWT) does not allow for self-consistency at the moment.
5.2. Polarization function¶
The polarization function gives the linear change in the electronic density of a non-interacting system with respect to changes in the effective potential. It is, thus, a fundamental quantity in the calculation of screening properties of a many-electron systems. For example, the dielectric function, instrumental in the calculation of spectroscopic quantities (e.g. EELS) and the screened interaction needed in GW, is related to the polarization matrix through \({\varepsilon(\mathbf{k},\omega)=1-P(\mathbf{k},\omega)v(\mathbf{k})}\), here given in matrix notation. The corresponding explicit formula for matrix elements of P in the mixed product basis is
A system without spin polarization has been assumed, hence the factor 2. In case of spin polarization, the formula has a spin summation instead of the factor 2 and corresponding spin quantum numbers. In the case of spin-orbit coupling (and no spin polarization), two spin summation labels are added, one in front of each “projection” \(\langle...\rangle\).
We have implicitly defined the spectral function S in Eq. (5), an explicit expression for which is basically given by the formula in the middle with the \({1/(\omega...)}\) replaced by \({\delta(\omega...)}\). (Technically, the \({M_{\mathbf{k}\mu}(\mathbf{r})}\) form the eigenbasis of the Coulomb matrix, so they are linear combinations of the mixed product basis functions.)
The expression for Eq. (5) involves an infinite empty-band summation over \({n'}\). In practice, this summation is truncated by the number of bands (keyword NBAND), which thus becomes an important convergence parameter. The self-energy contains an infinite band summation as well.
In principle, the k summation is infinite, too: In an infinite crystal, there are infinitely many k points, and the k summation formally turns into a k integration. In practice, of course, there can only be a discrete sampling of the Brillouin zone. The tetrahedron method enables a geometrical interpolation between the explicit k points and, thus, an approximate k integration. Therefore, the tetrahedron method is the default and recommended method. However, there are two other implemented methods: Simple summation over the k-point mesh (see HILBERT NONE) and the Gaussian method (see GAUSS).
5.2.1. HILBERT (SUSCEP)¶
The most important keyword in the calculation of the polarization function is HILBERT, which defines a (Hilbert) mesh for the frequency integration in Eq. (5). (The old keyword FSPEC still works but is deprecated.) The Hilbert mesh, used in conjunction with the tetrahedron and the Gaussian method, extends from the lowest (roughly the band gap) to the highest virtual electron transition energy. (Note that the spectral function is symmetric \({S(\omega)=S(-\omega)}\), which makes a mapping to \({\int_0^\infty...}\) possible.) The lower and upper bounds are, thus, predetermined by the input data. As the spectral function usually shows more variation at low energies (also, these energies are more important from a perturbation theory point of view), we employ an exponential mesh, which is dense at low and coarse at high energies. Two parameters are necessary to define the Hilbert mesh \({\{w_i\}}\), for example, the first step size \({\omega_2-\omega_1}\) and the stretching factor \({a=(\omega_{i+1}-\omega_i)/(\omega_i-\omega_{i-1})}\). These two parameters are accepted as real-valued arguments (example: HILBERT 0.01 1.04). However, with this definition it is not straightforward to increase the density of the mesh without changing the exponential form of the mesh. Therefore, it is recommended to use a different definition, namely using an integer as first argument (without a period!) and a real number as second (example: HILBERT 30 40.0; the second argument is always interpreted as real-valued, so HILBERT 30 40 is equivalent). The first argument gives the number of mesh points between 0 and 5 htr and the second argument is the “accumulated” stretching factor at 5 htr, i.e., by what factor the step size at 5 htr has increased from \({\omega_2-\omega_1}\). (The reason for defining an arbitrary but fixed energy of 5 htr is that modifying the energy range, e.g., by changing NBAND, then leaves the form of the Hilbert mesh unchanged.) In this way, increasing the first argument makes the mesh denser but does not affect the exponential form of the mesh, which, in turn, is governed by the second argument. So, there are two possible definitions (distinguished by whether the first argument has a period or not). For convenience, Spex always writes the equivalent parameters of the other definition to the output. By default, Spex uses a Hilbert mesh defined by HILBERT 50 30.0 for band-gap materials and HILBERT 150 50.0 for metals, unless a spectral frequency mesh is defined (e.g., DIELEC {0:1,0.01}), in which case Spex adjusts the Hilbert mesh to this frequency mesh. An idea of how well a given Hilbert mesh resolves the spectral function can be got by specifying WRITE INFO in the input file. Then, a file “spex.sf.nnn” (where nnn is a three-digit counting index) is written for each k point, and it contains the spectral function for the head element of P on the Hilbert mesh as plottable data. One can also define HILBERT NONE as a special option, which implements the k summation as simple sums over the k points without interpolation or broadening. HILBERT NONE is only available if the polarization function is to be calculated for purely imaginary frequencies (including zero).
HILBERT NONE |
Simple summation over k points. |
HILBERT 50 30.0 |
Use Hilbert mesh with fifty frequencies (between 0 and 5 htr) and an accumulated stretching factor of 30 at 5 htr. |
HILBERT 0.01 1.05 |
Use Hilbert mesh with a first step size of \({\omega_2-\omega_1=}\) 0.01 htr and a stretching factor of \({a=1.05}\). (First argument is real-valued.) |
5.2.2. MULTDIFF (SUSCEP)¶
(*) In the limit \({k\rightarrow 0}\), the projections in the numerator of Eq. (5) approach linearly to zero.
However, when calculating the dielectric function, one has to multiply with \({\sqrt{4\pi}/k}\) (square root of Coulomb matrix) in this limit.
So, the first order of \({\langle e^{i\mathbf{kr}} \phi_{\mathbf{q}n} | \phi_{\mathbf{k+q}n'} \rangle}\)
(corresponding to \({\mu=1}\)) in \(k\) becomes relevant. Using \(k\cdot p\) perturbation theory,
one can show that the linear term is proportional to \({(\epsilon_{\mathbf{q}n'}-\epsilon_{\mathbf{q}n})^{-1}}\).
This can lead to numerical problems if the two energies are very close to each other.
Therefore, when treating the \({\Gamma}\) point (\(k=0\)),
Spex multiplies the linear term with this energy difference, resulting in smooth and non-divergent values,
and takes the energy difference into account by replacing \({S(\omega)\rightarrow S(\omega)/\omega}\) in the frequency integration of Eq. (5),
thereby avoiding the numerical difficulties.
By default, Spex does that only at \(k=0\). The behavior can be changed with the keyword MULTDIFF in the section SUSCEP.
As an alternative, the energy differences can also be incorporated into the integration weights,
which is arguably even more stable numerically, see option INT below.
MULTDIFF OFF |
Never separate (divergent) energy differences. |
MULTDIFF ON |
Always separate energy differences (i.e., for all k points). |
MULTDIFF INT |
Use default behavior (separate for \(k=0\), do not for \(k\neq 0\)) but stick energy differences into integration weights. |
MULTDIFF INTON |
Always separate energy differences by sticking them into integration weights. |
5.2.3. PLASMA (SUSCEP)¶
(*) In the case of metals, the polarization function contains an additional term, the so-called Drude term, which gives rise to metallic screening (diverging static dielectric constant, short-range static W). The Drude term stems from virtual intraband transitions across the Fermi surface. It can be formulated with the square of the plasma frequency, which in turn is evaluated by an integration over the Fermi surface. The Drude term can
be treated analytically and, as long as the Fermi surface is sufficiently big, it normally does not pose a numerical problem. However, a very small Fermi surface eventually leads to a very sharp “Drude peak” in the GW self-energy, impeding a straight-forward numerical solution of the non-linear quasiparticle equation. One could also say that, while the Drude term is actually treated correctly, it gets too much weight because of the coarseness of the k-point mesh. It is, therefore, sometimes helpful to modify the plasma frequency. This is possible with the keyword PLASMA. Its argument replaces the plasma frequency calculated by the code. Setting PLASMA 0 switches the Drude term off altogether. Of course, PLASMA 0 thus also disables metallic screening, which might be unphysical. Therefore, there is a special option, PLASMA METAL, which scales the head element of \({W(\mathbf{k},\omega)}\) in the limit \({k\rightarrow 0}\) to enforce metallic screening. This latter option can be helpful, for example, in the case of semimetallic systems with a tiny Fermi surface.
PLASMA 1.5eV |
Set plasma frequency manually to 1.5 eV. |
PLASMA 0 |
Set plasma frequency to zero. Disables Drude term. |
PLASMA METAL |
Disable Drude term but enforce metallic screening by scaling the head element of W. |
5.2.4. CORES¶
By default, the n summation of Eq. (5) extends only over the valence states (represented in the LAPW basis) and excludes the core states.
The core states can be included in this summation in the same way as for the GW self-energy (see Section 5.1.18). If CORESOC is specified,
the SOC-splitted core states are included, otherwise the SOC-averaged core states (see Section 4.2.2). In the former case, the Weiss field
of a spin-polarized system can further lift the degeneracies. This is taken into account as well. See Section 5.1.18 for details and examples.
5.2.5. TETRAF (SUSCEP)¶
(*) In rare cases, especially for very large k-point sets, the determination of the tetrahedron weights (Timing wghts) can become computationally expensive. This is because Spex calculates tetrahedron weights for all k points by default, which makes it possible to average over equivalent k points, thereby avoiding a (slight) symmetry breaking connected with the spatial form of the tetrahedra. (The tetrahedra are not unique!) One can disable this averaging by setting TETRAF in the section SUSCEP. If set, tetrahedron weights are only calculated for the irreducible part of the BZ. This accelerates the calculation of the weights but introduces slight deviations due to symmetry breaking.
5.2.6. WGHTTHR (WFPROD)¶
(*) In both tetrahedron and Gaussian methods, integration weights are calculated to perform the k summation. To be more precise, an integration weight is calculated for each virtual transition, i.e., for each combination of band index pair (occ-nocc) and k point. One can reduce the number of terms by introducing a threshold value below which the respective weight is neglected. The corresponding keyword is WGHTTHR in the section SUSCEP. The default value is \({10^{-10}}\). It is usually not necessary to change this value in practice.
5.2.7. GAUSS¶
(*) The Gaussian method is included mostly for testing. It does not only affect the polarization function but also all other k summations (such as for the Hartree-Fock exchange potential and the determination of the Fermi energy). Therefore, GAUSS is a global keyword. It effectively replaces each single-particle eigenvalue by a Gaussian function with a certain width so that the density of states becomes a smooth function. In the calculation of the polarization function, one additionally needs a finite width for the Fermi edge. The keyword GAUSS needs the two width parameters as arguments given as real positive values. The advantage of the Gaussian method is its relative mathematical simplicity compared to the tetrahedron method and, in particular, that the Gaussian method cannot give rise to symmetry breaking.
GAUSS 0.001 0.01 |
Use Gaussian k-integration method with widths 0.001 and 0.01 htr. (Mostly used for testing.) |
5.2.8. DISORDER (SUSCEP)¶
(*) Mathematically, the parameter \({\eta}\) in (5) is a positive infinitesimal ensuring the correct time order of the response quantity. Spex effectively treats it as an infinitesimally small positive parameter. Sometimes, however, it can be useful to use a finite value for \({\eta}\), e.g., to simulate disorder in a material. This is possible with the keyword DISORDER in the section SUSCEP. Note that this keyword has rarely been used so far.
DISORDER 1000 |
Use a finite value \({\eta=1/(2\cdot 1000)\,\mathrm{htr}}\). |
5.3. Spectra¶
The dielectric function \(\epsilon_{\mathbf{GG}'}(\mathbf{k},\omega)\) is related to several spectroscopic experimental techniques where the system is perturbed (excited) by some incoming beam of particles but does not lose or gain particles (in contrast to photoemission, for example, where electrons are lost from the sample).
In optical spectroscopy measurements, the absorption cross section is proportional to the imaginary part of the long-wavelength macroscopic dielectric function \(\varepsilon_{M}(\omega)\), which can be obtained from the microscopic dielectric function by
Here, \(\varepsilon^{-1}\) refers to the matrix inverse.
Another example is electron-energy loss spectroscopy (EELS), where the scattering cross section can be shown to be proportional to the head element (\(\mathbf{G}=\mathbf{G}'=0\)) of the inverse dielectric function
Spex can be used to calculate the dielectric function. The respective job is called DIELEC. Arguments are expected to define
the k point index or label and a frequency range. For example, JOB DIELEC X:{0:1,0.001} would yield the dielectric function
evaluated at the X point between 0 and 1 htr in steps of 0.001 htr. Two files are written, “dielec” and “dielecR”, containing the
head elements of the (bare) dielectric function \(\varepsilon_\mathbf{00}(\mathbf{k},\omega)\) and of the renormalized
dielectric function \(1/\varepsilon^{-1}_\mathbf{00}(\mathbf{k},\omega)\). The imaginary part of the latter can directly be
identified with an optical absorption spectrum (excluding excitonic effects).
For the EELS spectrum, one would have to plot the imaginary part of the respective
reciprocal value (for example, in “gnuplot”: plot "dielecR" using 1:(imag(1/($2+{0,1}*$3)))).
Alternatively, the frequency mesh can be provided through a file, e.g., DIELEC X:"my_frequency_file". The file should contain
a list of frequencies, one frequency per line. Complex frequencies can be defined by, e.g., (1,0.2) (\(=1+0.2i\)).
Comments (# ...) and empty lines are allowed.
In the same way, other quantities can be calculated: the polarization function with SUSCEP (written to the file “suscep”), the renormalized polarization
function (\(R=P+PvR\)) with SUSCEPR (written to the file “suscepR”; “suscep” is also written), the screened interaction with
SCREEN (written to the file “screen”). In the first case (SUSCEP), one can also specify spin indices. For example,
JOB SUSCEP X:ud{0:1,0.001} restricts the polarization function to virtual up\(\rightarrow\)down transitions.
Other valid spin labels are uu, dd, du, and + (spin summed, default).
Since a dielectric matrix (or susceptibility, screened interaction etc.)
is calculated for each frequency (e.g., thousand frequencies in the case of {0:1,0.001}),
the memory demand can be very large for big systems. In such a case, it makes sense to divide the job into several smaller jobs.
This can be done by hand (example: JOB DIELEC X:{0:0.499,0.001} X:{0.5:1,0.001}) but also by a special adjunct to the definition of the frequency
range. For example, JOB DIELEC X:{0:1,0.001}/2 would give the same subdivision as the previous example.
By default, only the head element is written to the output files. More elements can be written using, e.g.,
JOB SUSCEP 1:{0.5eV:2eV,0.001eV},OUT=4, which would yield \(4\times 4\) matrices instead of only the head element.
One can also write the full matrix to a binary file with ...,OUT=BIN.
The special + k-point label can be used as well (e.g., JOB SUSCEP +:{0..50eV,0.01eV}). This enables using the script
“spex.band” to prepare a whole list of spectra for a series of Bloch vectors on a high-symmetry line. As explained in
Section 5.1.16 for the file “spectral”, the script appends a three-digit counting index to the name of the output file
(“suscep” in the present example, which is thus renamed to “suscep001”, “suscep002”, …). The data can then be compiled
into a single file using the “spex.extr” utility. (See Section 5.1.16 for details).
5.4. Total xc energies¶
Spex can calculate total exchange and correlation energies of the many-electron system. The total exchange energy is defined by the Hartree-Fock expression
The corresponding job is called HFENE. Internally, it works very much like a HF calculation. So, all parameters pertaining to HF
are available to HFENE, as well. However, the final result is a single number, \(E^\mathrm{x}\).
The total correlation energy can be calculated using the adiabatic-connection fluctuation-dissipation theorem (ACFDT) with the random-phase approximation (RPA) for the (partially renormalized) response function \(\chi_\lambda\) (\(\lambda=[0,1]\)). This response function is identical to the polarization function \(P\) (Section 5.2) for \(\lambda=0\) and to the “renormalized polarization function” \(R\) mentioned in Section 5.3 for \(\lambda=1\).
The ACFDT method gives the following form of the correlation energy functional
where \(\chi_0\) corresponds to the (bare) polarization function [Eq. (5)] and \(\chi_\lambda\) is a partially renormalized response function (i.e., with a scaled electron-electron interaction) fulfilling
here written in the general form including the (scaled) exchange-correlation kernel \(f_{\mathrm{xc},\lambda}\). For RPA, \(f_{\mathrm{xc},\lambda}=0\).
The evaluation of Eq. (7) requires the polarization function to be calculated for all
(irreducible) k points on an imaginary frequency mesh. The procedure is thus similar to a one-shot GW calculation
and needs a similar computation time. Many of the parameters discussed in connection with the GW method
(e.g., details related to the calculation of the polarization function, Section 5.2)
can be used for ACFDT-RPA in the same way. In particular, the same rules using the RESTART option (Section 5.1.13) apply.
It is, for example, possible to reuse the file “spex.cor” obtained from a previous GW calculation for an ACFDT-RPA calculation.
A run with RPAENE comprises the calculation of the total exchange energy using Eq. (6).
5.5. Interaction parameters (Hubbard U)¶
In a many-electron system, the electrons are correlated with each other through the Coulomb interaction. The motion of one electron depends on the dynamics of all others. The Coulomb interaction is thus responsible for the fact that we have to deal with a highly complex many-body problem. DFT takes electronic correlation into account, but most of the available functionals are suitable only for weak to moderate correlation. One way to go beyond standard DFT is by many-body perturbation theory, for example, using the GW approximation. However, this approach has its limits for very strong electronic correlations as in Mott insulators, for example.
As an alternative, one can resort to methods with a special treatment of local correlations, for example, the so-called LDA+U scheme, in which the local-density approximation (LDA) of DFT is augmented by an on-site Coulomb repulsion term and an exchange term with the Hubbard U and Hund exchange J parameters, respectively.
A more elaborate computational scheme, which combines many-body model Hamiltonian methods with DFT, is the so-called LDA+DMFT method. In this scheme, the interacting many-body system is mapped onto the subspace of localized states, for example, formed by d orbitals. The subspace contains much less electrons and can thus be treated with high-level quantum many-body approaches such as quantum Monte Carlo, numerical renormalization group, diagrammatic techniques, exact diagonalization, et cetera.
The other electrons, not included in the subspace, cannot simply be ignored. For example, their screening processes lead to a renormalization of the effective electron-electron interaction that acts in the subspace, again giving rise to the parameters U and J. Thus, the Coulomb interaction parameters play a crucial role in the study of the correlation effects in solids.
There are two ways to obtain the Hubbard U parameter from first principles, constrained local-density approximation (cLDA) and constrained random-phase approximation (cRPA). The latter is implemented in the Spex code and relies on the fact that, since the electrons outside the localized subspace can be assumed delocalized, the random-phase approximation should be appropriate for describing their screening contribution. The cRPA offers an efficient way to calculate the effective Coulomb interaction parameters in solids. Moreover, cRPA allows individual Coulomb matrix elements to be determined, e.g., on-site, off-site, intra-orbital, inter-orbital, and exchange, as well as their frequency dependence.
This is a minimal example input file for a Hubbard U calculation (here, employing a \(4\times 4\times 4\) k-point set):
BZ 4 4 4
JOB SCREENW {0}
SECTION WANNIER
ORBITALS 1 8 (d)
END
SECTION SUSCEP
HUBBARD
END
The section WANNIER contains the parameters for the construction of the Wannier functions, see Section 6.3.
(Note that the present values an example!)
The Wannier set spans the correlated subspace. Without HUBBARD, Spex would calculate parameters for the fully screened
interaction instead of the partially screened Hubbard U interaction. See below for further details.
5.5.1. JOB SCREENW …¶
In general, the bare and (fully or partially) screened interaction is calculated in reciprocal
space and represented in the mixed product basis (Section 6.2). The job definition SCREENW tells Spex
to project this interaction potential onto the set of local Wannier functions defined in the section WANNIER
(Section 6.3). The resulting interaction matrix elements
are written to the file “spex.cou” for the bare interaction (\(V=v\)) and the screened interaction
(\(V=U\) if HUBBARD is specified, otherwise \(V=W\), see below).
In addition, if \(\omega=0\) is included in the frequency mesh,
effective interaction parameters (Hubbard-Hund and/or Kanamori parameterization) are
written to the output file for both the bare (v) and the screened interaction (U or W).
(Note again that, without the keyword HUBBARD, the effective parameters are obtained from the fully screened interaction W
and would thus be unsuitable for a Hubbard model Hamiltonian.)
The Hubbard-Hund parameters are given for each complete
Wannier \(l\) shell (e.g., specifying (d) in ORBITALS defines the complete d shell, see Section 6.3),
here written for the partially screened interaction U,
The Kanamori parameters are given for groups of t2g (\(N=3\)) or eg orbitals (\(N=2\)) as
In the case of a spin-polarized system, the spin-up and spin-down Wannier functions differ slightly, and the respective spin-indices
have to be specified in the job definition using one of the labels uu, dd, du, or + (spin summed). There is no default.
JOB SCREENW {0:40eV,0.1eV} |
Calculate \(W(\mathbf{r},\mathbf{r}';\omega)\) [\(U(\mathbf{r},\mathbf{r}';\omega)\) if HUBBARD is specified] and project it onto the Wannier functions; {…} defines the frequency mesh. |
JOB SCREENW {0} |
The same only for the static case \(\omega=0\). (Here, {0} is short for {0:0,1}.) |
JOB SCREENW uu{0} |
The same for the spin-polarized case: the up-up combination of Wannier functions is selected. |
5.5.2. HUBBARD (SUSCEP)¶
With the keyword HUBBARD (section SUSCEP), the screening that takes place in the correlated subspace is eliminated from the screened interaction, thus
yielding the partially screened interaction and, with JOB SCREENW ..., the effective interaction parameters
for a Hubbard model Hamiltonian. The correlated subspace is spanned by the Wannier functions. So, the Wannier definition affects the
calculation in two ways: (1) It defines the local Wannier basis on which the (bare and) partially screened interaction is
projected, and (2) it spans the subspace whose screening is eliminated. Sometimes it makes sense to separate these two
effects, for example, if the subspace is spanned by Wannier functions located at several (possibly symmetry-equivalent) atoms,
but the effective parameters are only needed for one of the atoms (on-site interactions). Such a calculation is performed in two steps
with a file name as argument (example: HUBBARD hub). In the first step (i.e, the file does not exist yet),
one specifies the full set of Wannier functions. When Spex is run, it writes information about the screening contribution
that takes place in the correlated subspace (and that is to be eliminated) to the specified file (“hub”) and stops.
Before the second run, one can modify the Wannier definition (e.g., with the keyword SUBSET). In the
present example, one would reduce the Wannier set (to the orbitals located at one and the same atom). The second Spex run then calculates
the partially screened interaction and projects it onto the reduced set of Wannier functions.
HUBBARD |
Calculate Hubbard U interaction matrix including effective parameters. |
HUBBARD hub.dat |
Write information about subspace screening to “hub.dat”, if the file does not exist, and calculate the Hubbard U interaction matrix using data from “hub.dat” otherwise. |
5.5.3. RESTART¶
Since SCREENW calculations can be quite costly, the keyword RESTART enables a restart of a calculation that has stopped before
finishing. The usage is similar to GW calculations (Section 5.1.13). The file “spex.cor” contains the (fully or partially) screened
interaction for each (completed) k point, and the file “spex.wcou” holds the last update of the projected interaction matrix.
The logical table is similar to Section 5.1.13. (See Section 4.1.7 for more details.)
spex.cor |
spex.wcou |
|
|---|---|---|
| – | – | write |
RESTART |
read-write | write |
RESTART 2 |
read-write | read-write |
5.5.4. DISENTGL (WANNIER)¶
(*) There are different ways to eliminate the screening channels in the case of an entangled band structure, i.e., if the
correlated subspace is not made up of isolated bands. In this case, it is not possible to unambiguously define the screening
that takes place only in the subspace. The default approach of Spex,
described in [Phys. Rev. B 83, 121101 (2011)], scales each virtual transition \(\phi\rightarrow\phi'\) by the probability that the
transition takes place in the subspace. (To be more precise, it is the probability that the electron-hole pair
occupying the states \(\phi\) and \(\phi'\) happens to be in the subspace.) There is another method,
called disentanglement method [Phys. Rev. 80, 155134 (2009)],
in which the reference mean-field system is modified in such a way that each state \(\phi\) is either fully contained in
the subspace or completely outside (corresponding to probabilities 1 or 0). This method can be used by specifying DISENTGL
in the section WANNIER.
Warning
Using this keyword actually modifies the mean-field system! (The keyword has not been tested thoroughly yet.)
5.5.5. RSITE (WANNIER)¶
(*) The interaction parameters are calculated between Wannier orbitals located at the atoms of the first unit cell.
Let us denote two site position vectors as \(\mathbf{r}_1\) and \(\mathbf{r}_2\). We have on-site parameters for
\(\mathbf{r}_1=\mathbf{r}_2\) and off-site parameters for \(\mathbf{r}_1\neq\mathbf{r}_2\) (which is, of course, possible only
for a multi-atom basis).
However, one of the atoms, say the first, can also be located in a
different unit cell shifted by a lattice vector \(\mathbf{R}\), i.e., at the position \(\mathbf{r}_1+\mathbf{R}\),
which gives rise to another class of off-site interaction parameters (which exists also for a single-atom basis).
The keyword RSITE can be used to define the lattice vectors \(\mathbf{R}\). The following examples show the syntax.
RSITE (0,0,1) (0,1,1) (1,1,1) |
Defines three lattice vectors. If (0,0,0) is not included explicitly, as in the present example, it is prepended to the list automatically. |
RSITE (0,0,0)-(0,5,10) |
Defines the vectors (0,0,0), (0,1,2), (0,2,4), …, (0,5,10). |
RSITE (0,0:2,0:2) |
Defines the vectors (0,0,0), (0,0,1), (0,0,2), (0,1,0), …, (0,2,2). |
5.5.6. WBLOCH (WANNIER)¶
(*) The evaluation of the interaction parameters involves projections of the form
\(\langle M_{\mathbf{k}\mu} w_{\mathbf{q}n} | w_{\mathbf{k+q}n'} \rangle\),
where \(M_{\mathbf{k}\mu}(\mathbf{r})\) are the functions of the mixed product basis (see Section 6.2),
in which the screened (bare) interaction potential is expanded, and \(w_{\mathbf{k}n}(\mathbf{r})\) are the Wannier Bloch
functions (corresponding to Eq. (1) of Section 6 without the \(\mathbf{k}\) summation).
Until version 05.03., the coefficients for the latter (with respect to the LAPW basis) were constructed explicitly.
Since version 05.04., these coefficients are not used anymore, and we instead compute
\(\langle M_{\mathbf{k}\mu} \phi_{\mathbf{q}m} | \phi_{\mathbf{k+q}m'} \rangle\)
with the single-particle eigenfunctions \(\phi_{\mathbf{k}m}(\mathbf{r})\),
allowing the symmetry properties of the eigenfunctions to be exploited to speed up the calculation.
To this end, irreducible representations are employed.
The Wannier expansion coefficients \(U_{\mathbf{k}m,n}\) are multiplied later.
The Wannier set, on the other hand, is not guaranteed to reflect the full symmetry of the system.
The new algorithm is substantially faster than the old one, in particular, for large k-point sets,
if the system is highly symmetric. Furthermore, the new algorithm has less restrictions than the old one.
For example, it can be used in conjunction with MAXIMIZE and SUBSET (and without STOREBZ) in contrast to
the old algorithm. However, if, on the other hand, the system has only low symmetry and/or the
number of Wannier functions (index \(n\)) is much smaller than the
number of eigenstates (index \(m\)) from which the Wannier set is
constructed, then the old algorithm might be more efficient. In addition, slight distortions of the system
can make the usage of irreducible representations critical, in which case the old algorithm should be used.
(Also see keyword NOSYM, Section 4.2.10.) The old algorithm can still be used with the keyword WBLOCH.
Note
Paragraphs discussing advanced options are preceded with (*), and the ones about obsolete, unmaintained, or experimental options are marked with (**). You can safely skip the paragraphs marked with (*) and (**) at first reading.